13+ time derivative of a vector in a rotating coordinate system
An example is a pair of separate circles. In addition the notion of direction is strictly associated with the notion of an angle between two vectors.

Kinematics Derivative Of A Rotating Vector In Cylindrical Coordinates Engineering Dynamics Mechanical Engineering Mit Opencourseware
And then were done we found the normal vector.
. The reference point analogous to the origin of a Cartesian coordinate system is called the pole and the ray from the pole in the reference direction is the polar axis. Where G μν is the Einstein tensor is the metric tensor T μν is the stressenergy tensor Λ is the cosmological constant and κ is the Einstein gravitational constant. The Einstein tensor is defined as where R μν is the Ricci curvature tensor and R is the scalar curvatureThis is a symmetric second-degree tensor that depends on only the metric tensor and its first and second.
We start by taking the normalized vector for the derivative at some point on the curve. Taking a time derivative the velocity of the particle is. For a time-invariant magnetic field it tends to align with the field.
Cartesian cylindrical and spherical. Since photons travel at the speed of light their world lines have a slope of 1. If the dot product of two vectors is defineda scalar-valued product of two vectorsthen it is also.
The total energy of a system can be subdivided and classified into potential energy kinetic energy or combinations of the two in various ways. In this way we realized the free control of an extremely strong actuation magnetic field B a by a very weak magnetic field B b. In 3-dimensional orthogonal coordinate systems are 3.
The center of force O can be chosen as the origin of a coordinate system. Instead of forces Lagrangian mechanics uses the energies in the system. Specifically for a dynamic rotating field the SPM will follow the field with a fixed misalignment angle 90.
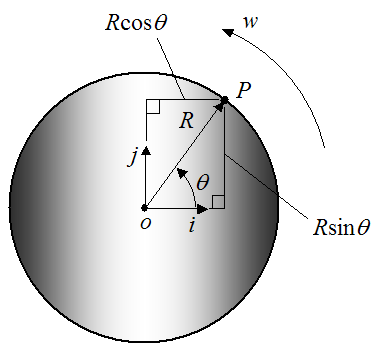
If m is an objects mass and v is its velocity also a vector quantity then the objects momentum p is. We normalize it so the maths is less work. Introduce the unit vectors ȷ representing standard unit basis vectors in the rotating frame.
In Newtonian mechanics linear momentum translational momentum or simply momentum is the product of the mass and velocity of an object. Sets the given vector result with the coordinates of value if the vector value is in the cube defined by the vectors min and max If a coordinate value of value is lower than one of the min coordinate then this value coordinate is set with the min one If a coordinate value of value is greater than one of the max coordinate then this value coordinate is set with the. The above-mentioned triad of unit vectors is also called a basisSpecifying the coordinates components of vectors of this basis in its current rotated position in terms of the reference non-rotated coordinate axes will completely describe the rotationThe three unit vectors and that form the rotated basis each consist of 3 coordinates yielding a total of 9 parameters.
The magnitude of the pseudovector represents the angular speed the rate at which the object. Applies to each particle. Kinetic energy is determined by the movement of an object or the composite motion of the components of an object and potential energy reflects the potential of an object to have motion and generally is a function of the.
We can use the cross product a second time and immediately get our normal vector. The central quantity of Lagrangian mechanics is the Lagrangian a function which summarizes the dynamics of the. This two-fold definition may be expressed mathematically as follows.
Generally units are measured in pixels. Thus a line segment without its end points is a manifoldThey are never countable unless the dimension of the manifold is 0Putting these freedoms together other examples of manifolds are a parabola a hyperbola and the locus of points on a cubic curve y 2. Notice that velocity always points in the direction of motion in other words for a curved path it is the tangent vectorLoosely speaking first order derivatives are related to.
The left-hand side is the time derivative of the momentum and the right-hand side is the force represented in terms of the potential energy. Expressing the NavierStokes vector. Browse our listings to find jobs in Germany for expats including jobs for English speakers or those in your native language.
As an aside the unit vectors u j cannot change magnitude so derivatives of these vectors express only rotation of the coordinate system B. The vector r joining O to the present position of the particle is known as the position vector. In the geometrical and physical settings it is sometimes possible to associate in a natural way a length or magnitude and a direction to vectors.
It works as a two-dimensional x-y plane. From the instantaneous position r rt instantaneous meaning at an instant value of time t the instantaneous velocity v vt and acceleration a at have the general coordinate-independent definitions. In general spacetimes the coordinate system x α is arbitrary the covariant derivative α the Ricci tensor R αβ and raising and lowering of indices are defined by the Lorentzian metric g αβ and the dAlembert operator is defined as α.
This is the derivative of the momentum 4-vector with respect to. A Fourier transform FT is a mathematical transform that decomposes functions depending on space or time into functions depending on spatial frequency or temporal frequencyThat process is also called analysisAn example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitchesThe term Fourier transform refers to. For an N particle system in 3 dimensions there are 3N second order ordinary differential equations in the positions of the particles to solve for.
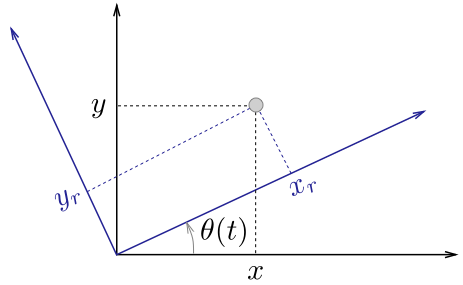
As we move right from there x increases. Suppose the frames are aligned at and the -axis is the axis of rotationThen for a counterclockwise rotation through angle. The dAlembert operator on Minkowski space is α α as in the vector formulation.
It is a vector quantity possessing a magnitude and a direction. In mathematics the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The origin where x0 and y0 is the upper left-hand corner.
The vertical time coordinate is scaled by so that it has the same units meters as the horizontal space coordinate. The time-derivatives of these unit vectors are found next. The domain for these equations is commonly a 3 or less Euclidean space for which an orthogonal coordinate reference frame is usually set to explicit the system of scalar partial differential equations to be solved.
In physics angular velocity or rotational velocity ω or Ω also known as angular frequency vector is a pseudovector representation of how fast the angular position or orientation of an object changes with time ie. In the Cartesian coordinate system these are called x y. Therefore a central force must have the mathematical form.
General relativity also known as the general theory of relativity and Einsteins theory of gravity is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physicsGeneral relativity generalizes special relativity and refines Newtons law of universal gravitation providing a unified description of gravity as a. How quickly an object rotates or revolves relative to a point or axis. Euclidean and affine vectors.
The default coordinate system in SVG is much the same as in HTML. Rotating coordinates is actually very easy if you know the rule for it. In the International System of Units SI the unit of measurement of.
737 Landau and Lifshitz argue that the Lagrangian formulation makes the conceptual content of classical mechanics more clear than starting with Newtons laws. On the other hand vector X AB simply locates the origin of frame B relative to frame A and so cannot include rotation of frame B. Earths magnetic field also known as the geomagnetic field is the magnetic field that extends from Earths interior out into space where it interacts with the solar wind a stream of charged particles emanating from the SunThe magnetic field is generated by electric currents due to the motion of convection currents of a mixture of molten iron and nickel in Earths outer core.
Manifolds need not be connected all in one piece. As we move downward y increases. Manifolds need not be closed.
This result can be obtained from a rotation matrix.
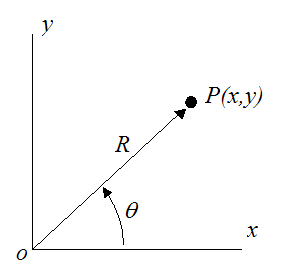
Vector Derivative

Vector Derivative

Time Derivatives In Inertial And Rotating Frames 9 3 Youtube

Pdf Irodov Problems In General Physics Lokesh Khandelwal Academia Edu

Experiment 1 Reconstruction Of The Ogorodnikov Milne Model Parameters Download Table

Time Derivatives Of Unit Vectors For Polar Coordinates Full Derivation 2d Coordinate Systems Youtube
Rotating Coordinate System
Honors Physics Weekly Notes

Rotation Matrices Derivation Of Spherical Coordinates Via Multiple Rotations Youtube

First Order Perturbative Calculation Of The Frequency Shifts Caused By Static Cylindrically Symmetric Electric And Magnetic Imperfections Of A Penning Trap Sciencedirect
Quick Question Rate Of Change Of A Rotating Vector Physics Forums

Time Derivatives In Inertial And Rotating Frames 9 3 Youtube

Newtonian Mechanics The Time Derivatives Of Vectors In Rotating Frames Physics Stack Exchange

Vector Derivatives The Equation Of Coriolis And The Angular Velocity Vector Youtube

Protein Ensembles How Does Nature Harness Thermodynamic Fluctuations For Life The Diverse Functional Roles Of Conformational Ensembles In The Cell Chemical Reviews

Chapter 13 Vector Functions
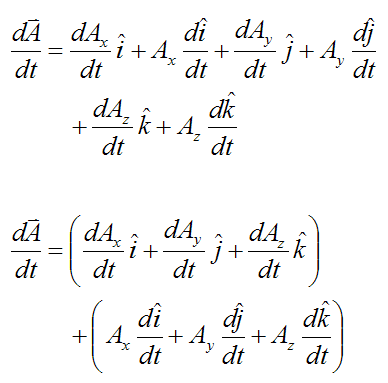
Vector Derivative